Cryptanalyse Linéaire d'un AES-128

February 24, 2023 - 10 mins read

crypto
tuto

Introduction

AES est un chiffrement par bloc basé sur des opérations matricielles élémentaires. Avant de s’attaquer à tout ce système, il est important de les avoirs en tête. Voici donc une explication rapide sur le mode de fonctionnement d’AES.

Présentation rapide d’AES

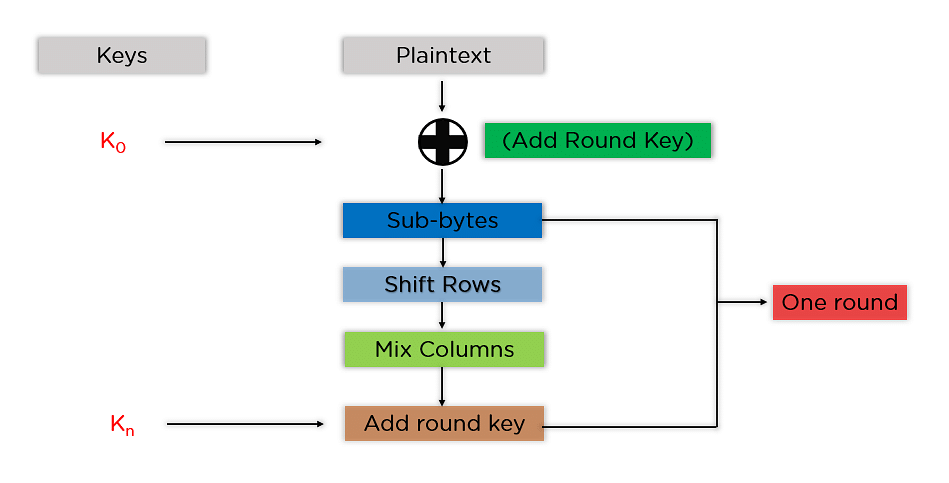
On souhaite chiffrer un bloc se 16 bytes, la première étape est de l’exprimer sous la forme de matrice 4*4:

$$ \begin{pmatrix} 1 & 2 & 3 & 4 \newline 5 & 6 & 7 & 8 \newline 9 & 10 & 11 & 12 \newline 13 & 14 & 15 & 16 \newline \end{pmatrix} $$ Cette matrice va subir plusieurs modifications. On définit un round par l’enchainement des opérations :

Sub-Bytes
Shift Rows
Mix Collumns
Add Round key

La matrice initial subit d’abord une opération Add Round Key avant d’effectuer les tours: Ces opérations sont répétées 10 fois pour un AES classique.

Alt text

Linéarité des opérations.

Les opérations :

Shift Rows
Mix Collumns
Add Round key sont linéaires , on peut exprimer chacune de ces opérations de la forme:
$\forall i \in {1,2,3}~|~~\phi_i:x \to A_i*X+B_i$

La dernière opération, Sub-Bytes elle ne l’est pas.Cela empêche la cryptanalyse linéaire d’un tel système.

L’opération Sub-Bytes:

Cette opération consiste à associer à chaque byte de la matrice d’entrée, un unique autre byte déterminé par un mapping appelé Sbox:

$$ \begin{pmatrix} 1 & 2 & 3 & 4 \newline 5 & 6 & 7 & 8 \newline 9 & 10 & 11 & 12 \newline 13 & 14 & 15 & 16 \newline \end{pmatrix} $$

devient

$$ \begin{pmatrix} Sbox(1) & Sbox(2) & Sbox(3) & Sbox(4) \newline Sbox(5) & Sbox(6) & Sbox(7) & Sbox(8) \newline Sbox(9) & Sbox(10) & Sbox(11) & Sbox(12) \newline Sbox(13) & Sbox(14) & Sbox(15) & Sbox(16) \newline \end{pmatrix} $$

Cette opération rend le chiffrement non-linéaire !

Si on supprime cette opération ou qu’on utilise une S-box linéaire, on casse cette propriété qui rend notre chiffrement complètement vulnérable à de nouvelles techniques d’attaques !
Exemple de SBOX vulnérable: ($\forall i \in [0,255]~|~~Sbox(x)=x$)

Analyse Linéaire:

Comme évoqué précédemment , les 3 autres opérations d’AES sont linéaires , une combinaison de celle-ci (round) conserve cette propriété ce qui permet d’écrire en écriture matricielle:

$AES(P)=A*P+B$

avec :

A une matrice de 16*16 bytes = 128*128 bits.
B un vecteur colonne de 128 bits.
P, notre texte en clair , un vecteur de 128 bits.

Un fait notable est que la matrice A ne dépend pas de la clé utilisé. Seul B en est dérivé.
On peut donc tenter de récupérer la clé utilisé par cette AES .

Attaque du système.

Premières partie.

La première étape est de retrouver la matrice B Pour ce faire, on peut procéder de 2 façons:

Première méthode :

La première technique est de demander à chiffrer 16 bytes nuls, on aura alors l’égalité suivante :

$$ AES(\begin{pmatrix} 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline \end{pmatrix}) = \begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} & a_{1,4} \newline a_{2,1} & a_{2,2} & a_{2,3} & a_{2,4} \newline a_{3,1} & a_{3,2} & a_{3,3} & a_{3,4} \newline a_{4,1} & a_{4,2} & a_{4,3} & a_{4,4} \newline \end{pmatrix}*\begin{pmatrix} 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline \end{pmatrix}+\begin{pmatrix} b_1 \newline b_2 \newline b_3 \newline b_4 \newline b_5 \newline b_6 \newline b_7 \newline b_8 \newline b_9 \newline b_{10} \newline b_{11} \newline b_{12} \newline b_{13} \newline b_{14} \newline b_{15} \newline b_{16} \newline \end{pmatrix}=\begin{pmatrix} b_1 \newline b_2 \newline b_3 \newline b_4 \newline b_5 \newline b_6 \newline b_7 \newline b_8 \newline b_9 \newline b_{10} \newline b_{11} \newline b_{12} \newline b_{13} \newline b_{14} \newline b_{15} \newline b_{16} \newline \end{pmatrix}=B $$

Seconde méthode :

La seconde méthode consiste à travailler avec des matrices 128*128
Comme on cherche à casser le chiffrement AES, on place toutes nos opérations dans $GF(2)$ , ainsi :

1+1 = 0
1-1 = 0
En résumé, les opérations +/- sont remplacé par le xor $\oplus$ On pose : $$ X = \begin{pmatrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \newline 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \newline 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \newline 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \newline 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \newline 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \newline 1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \newline 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \newline \end{pmatrix} $$ $$ I = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \newline 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \newline 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \newline 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \newline 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \newline 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \newline 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \newline 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \newline \end{pmatrix} $$ Puis : $$ C = \begin{pmatrix} X & X+I & I & I \newline X & X & I+I & I \newline X & X & I & I+I \newline X+I & X & I & I \newline \end{pmatrix} $$ C’est l’équivalent matricielle de l’opération MixColumns sur une unique colonne

Et : $$ \sigma_0 = \begin{pmatrix} I & 0 & 0 & 0 \newline 0 & 0 & 0 & 0 \newline 0 & 0 & 0 & 0 \newline 0 & 0 & 0 & 0 \newline \end{pmatrix} ~, ~ \sigma_1 = \begin{pmatrix} 0 & 0 & 0 & 0 \newline 0 & I & 0 & 0 \newline 0 & 0 & 0 & 0 \newline 0 & 0 & 0 & 0 \newline \end{pmatrix} $$ $$ \sigma_2 = \begin{pmatrix} 0 & 0 & 0 & 0 \newline 0 & 0 & 0 & 0 \newline 0 & 0 & I & 0 \newline 0 & 0 & 0 & 0 \newline \end{pmatrix} ~, ~ \sigma_3 = \begin{pmatrix} 0 & 0 & 0 & 0 \newline 0 & 0 & 0 & 0 \newline 0 & 0 & 0 & 0 \newline 0 & 0 & 0 & I \newline \end{pmatrix} $$ On peut ainsi décrire l’opération Shit Rows: $$ S = \begin{pmatrix} \sigma_0 & \sigma_1 & \sigma_2 & \sigma_3 \newline \sigma_3 & \sigma_0 & \sigma_1 & \sigma_2 \newline \sigma_2 & \sigma_3 & \sigma_0 & \sigma_1 \newline \sigma_1 & \sigma_2 & \sigma_3 & \sigma_0 \newline \end{pmatrix} $$ Finalement, on peut écrire la matrice pour l’opération : Shift rows

$$ M = \begin{pmatrix} C & 0 & 0 & 0 \newline 0 & C & 0 & 0 \newline 0 & 0 & C & 0 \newline 0 & 0 & 0 & C \newline \end{pmatrix} $$ On prenant en compte cette notation, on représente un round de l’AES par la multiplication avec $M*S$ que l’on note $R$

On obtient finalement pour un AES-128 (10 rounds):
$A=S \oplus R ^9$

On peut donc exprimer B de cette manière :
$B=AES(P)-A\oplus P$ (Ici B est exprimé sous la forme d’une matrice 128*128 correspondant aux bits des 16*16=256 bytes qui la compose dans la première méthode.

On peut coder cette partie de cette manière :
(On utilise SageMaths)

from sage.all import *
from aes import myAES

class aes_linear:
	def __init__(self,plaintext,ciphertext):
		# AES(P) = A*P+B
		self.P = self.plain2vect(plaintext)
		self.AES_P = self.plain2vect(ciphertext)
		self.recover_A()
		self.recover_B()

	def plain2vect(self,data):
		return vector([int(x) for x in "{:08b}".format(int(data.hex(),16)).zfill(128)])

	def vect2plain(self,data):
		k = int(''.join([str(x) for x in data]),2)
		return k.to_bytes((k.bit_length() +7) // 8, "big")

	def recover_A(self):
		I = matrix.identity(GF(2),8)
		Z = matrix(GF(2),8)
		X = matrix(GF(2),8,[
			[0,1,0,0,0,0,0,0],
			[0,0,1,0,0,0,0,0],
			[0,0,0,1,0,0,0,0],
			[1,0,0,0,1,0,0,0],
			[1,0,0,0,0,1,0,0],
			[0,0,0,0,0,0,1,0],
			[1,0,0,0,0,0,0,1],
			[1,0,0,0,0,0,0,0]
		])

		C = block_matrix([
			[X,X+I,I,I],
			[I,X,X+I,I],
			[I,I,X,X+I],
			[X+I,I,I,X],
		])

		sig0 = block_matrix([[I,Z,Z,Z],[Z,Z,Z,Z],[Z,Z,Z,Z],[Z,Z,Z,Z]])
		sig1 = block_matrix([[Z,Z,Z,Z],[Z,I,Z,Z],[Z,Z,Z,Z],[Z,Z,Z,Z]])
		sig2 = block_matrix([[Z,Z,Z,Z],[Z,Z,Z,Z],[Z,Z,I,Z],[Z,Z,Z,Z]])
		sig3 = block_matrix([[Z,Z,Z,Z],[Z,Z,Z,Z],[Z,Z,Z,Z],[Z,Z,Z,I]])

		S = block_matrix([
			[sig0,sig1,sig2,sig3],
			[sig3,sig0,sig1,sig2],
			[sig2,sig3,sig0,sig1],
			[sig1,sig2,sig3,sig0],
		])

		Z2 = matrix(GF(2),32)
		M = block_matrix([
			[C,Z2,Z2,Z2],
			[Z2,C,Z2,Z2],
			[Z2,Z2,C,Z2],
			[Z2,Z2,Z2,C],
		])

		R = M*S
		A = S*R**9

		self.R = R
		self.S = S
		self.A = A

	def recover_B(self):
		self.B = self.AES_P - self.A*self.P

	def break_key(self):
		I  = matrix.identity(GF(2),8)
		I2 = matrix.identity(GF(2),8*4)
		Z  = matrix(GF(2),8)
		Z2 = matrix(GF(2),8*4)

		T = block_matrix([
		    [Z,I,Z,Z],
		    [Z,Z,I,Z],
		    [Z,Z,Z,I],
		    [I,Z,Z,Z]
		])

		U = block_matrix([
			[I2,Z2,Z2,T],
			[I2,I2,Z2,T],
			[I2,I2,I2,T],
			[I2,I2,I2,T+I2],
		])

		V = U**10
		for i in range(10):
			V += self.S * (self.R**i) * (U**(9-i))
		V_inv = V.inverse()


		
		cipher = myAES()
		cipher.key = [0]*16
		cipher.subKeys = cipher.expandKey(cipher.key)
		K = cipher.encrypt(self.P)
		
		K = self.plain2vect(bytes(K))
		r = self.AES_P

		k = V_inv * (K + r).change_ring(GF(2))
		return self.vect2plain(k)

dec = b'\x00'*16
enc = encrypt_oracle(dec)
exp = aes_linear(
	plaintext  = dec,
	ciphertext = enc
)
key = exp.break_key()
print(key.hex())

Seconde Partie.

Une fois que B est exprimé, nous souhaitons en déduire la clé utilisée par l’AES. L’absence de l’opération Sub-Bytes implique que ce résidu est lui aussi linéaire. On a donc :
$B = C*{Clé}\oplus K$

L’objectif est donc de déterminer $C$ et $K$ afin de déduire la clé : ${Clé}=C^{-1}*(B \oplus K)$

Le vecteur K est le plus facile à trouver :
Il suffit d’implémenter cet AES vulnérable et de chiffrer le vecteur composé de 16 bytes nuls avec une clé , elle aussi nulle:

$$ K = AES(Clé=\begin{pmatrix} 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline \end{pmatrix},plain=\begin{pmatrix} 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline \end{pmatrix}) $$ Sur un AES-128 (10 tours) , on obtient :

K = [154, 2, 123, 81, 228, 247, 69, 129, 70, 80, 119, 23, 117, 152, 84, 249]

Pour l’expression de $C$ , voir ici : https://crypto.stackexchange.com/questions/89596/linear-aes-expression-of-k-in-aesp-apk

Autre méthode.

Une méthode plus simple semble être celle d’utiliser la bibliothèque Rijndael-GF, en effet celle-ci permet de recoder rapidement l’AES sans utiliser la S-box et nous pouvons ainsi utiliser des variables symbolique pour avoir une expressions des subkeys en fonction de la clé :

Nous devons aussi exprimer RCON sous la forme de polynôme dans $GF(2)$

RCON = [0]+[
      self.rgf._F('1'),
      self.rgf._F('x'),
      self.rgf._F('x^2'),
      self.rgf._F('x^3'),
      self.rgf._F('x^4'),
      self.rgf._F('x^5'),
      self.rgf._F('x^6'),
      self.rgf._F('x^7'),
      self.rgf._F('1 + x + x^3+ x^4'),
      self.rgf._F('x + x^2 + x^4 + x^5')
   ]

Ainsi avec un anneau de polynôme , on peut exprimer les subkeys:

from sage.crypto.mq.rijndael_gf import RijndaelGF
from sage.rings.polynomial.polynomial_ring_constructor import PolynomialRing

class Weak_Aes()
   def __init__(self):
      self.rijndaelGF = RijndaelGF(4, 4, key_chr='k')
      self.P = PolynomialRing(self.rijndaelGF._F,16,self.rijndaelGF.key_vrs.list())
      self.subK = self.key_schedule()
      
   def key_schedule(self): 
      xor = lambda a,b : [ a_ + b_ for a_, b_ in zip(a,b) ]
      Field_GF_2x8 = self.rijndaelGF._F
      RCON = [0x8d,
         Field_GF_2x8('1'),
         Field_GF_2x8('x'),
         Field_GF_2x8('x^2'),
         Field_GF_2x8('x^3'),
         Field_GF_2x8('x^4'),
         Field_GF_2x8('x^5'),
         Field_GF_2x8('x^6'),
         Field_GF_2x8('x^7'),
         Field_GF_2x8('x^4 + x^3 + x + 1'),
         Field_GF_2x8('x^5 + x^4 + x^2 + x')
      ]
   
      subK = [list(self.P.gens())]
      for rnd in range(10):
         last = subK[-1]
         a, b, c, d = last[-4:]
         x =  xor(last[0 : 4],[b+RCON[len(subK)],c,d,a])
         x += xor(last[4 : 8],x[-4:])
         x += xor(last[8 :12],x[-4:])
         x += xor(last[12:16],x[-4:])
         subK.append(x)
   
      subkeys = [column_matrix(4, 4, s) for s in subK]
      return subkeys

De cette manière, on obtient chaque subkeys sous forme polynomial dépendantes de 16 variables correspondantes aux 16 bytes de la clés.

Il ne reste plus qu’à réimplémenter l’AES avec les 3 opérations connues à travers RijndaelGF et à passer nos subkeys symboliques dans celui-ci. Finalement , une fois fait , on retrouve l’état de l’AES après chiffrement , il ne reste plus qu’à résoudre le système matricielle avec une paire (plaintext,ciphertext) quelconque.

Cf Ideals in multivariate polynomial rings