From ECC to Diffie-Hellman

Introduction

L’échange de clé de Diffie-Hellman est une méthode pour partager un secret entre 2 individus de manière sécurisé, même si leurs transmissions sont sur écoute.

Présentation des courbes elliptiques :

Avant de s’attaquer à la partie cryptographique, il est nécessaire de comprendre le fonctionnement global des courbes elliptiques.

Une courbe elliptique est un ensemble de points $(x,y)$ vérifiant une équation du type: $y^2=x^3+ax+b$, autrement dit , on définit une courbe elliptique comme :

• $E = {(x,y) \in K ~|~y^2=x^3+ax+b} \cup { O }$

• avec $\begin{cases} K \in {R,Q,C,Z/nZ } \newline (a,b) \in K \newline \Theta~,~un~point~à~l’infini \newline 4a^3+27b^2 \not = 0 \end{cases}$

Une chose notable est que les opérations élémentaires sont toutes modifiés.
En effet, si on prend deux points A et B de la courbe, il faut trouver un moyen pour que A+B le soit aussi.

On peut prendre l’exemple du corp des Réels: $K = R$

Voici une courbe elliptique: $a = -b = -1$

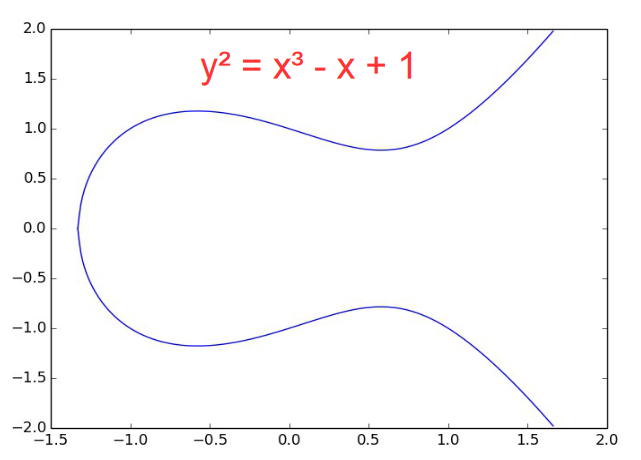
On y place 2 points P et Q :

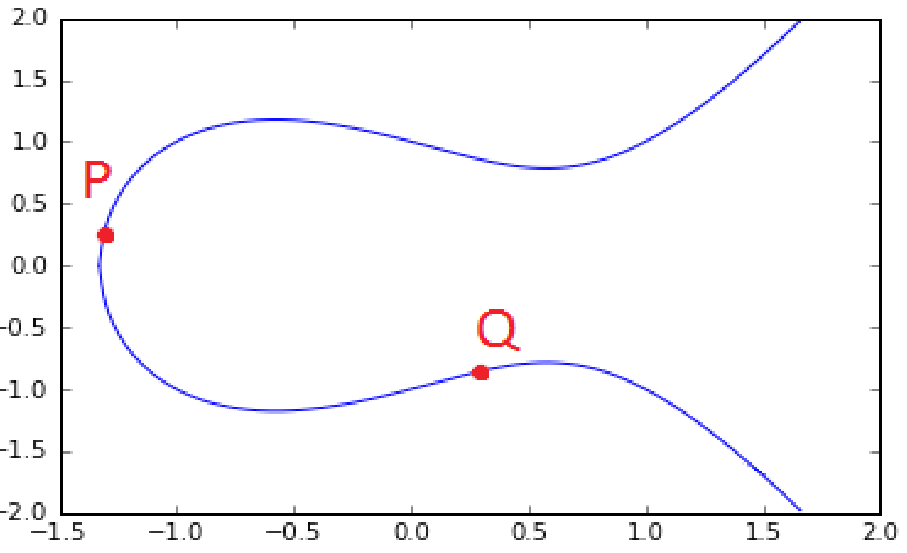
On définit donc le point $R$ tel que :

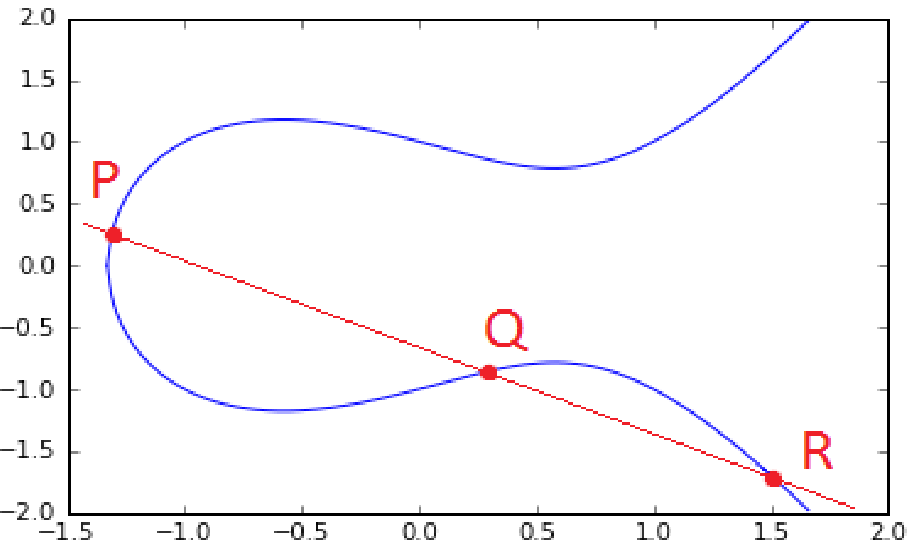
et enfin : $P+Q$ :

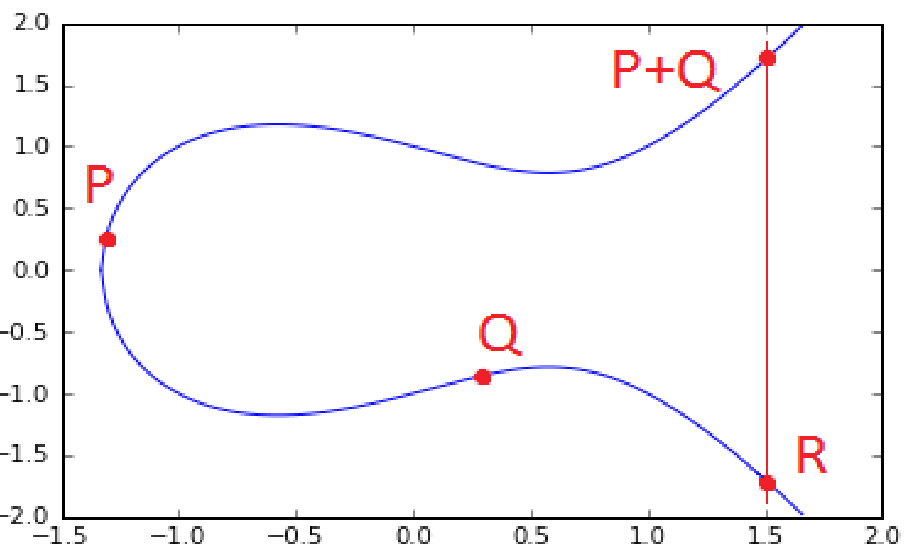
De manière algébrique :

On distingue 4 possibilités pour l’addition sur les courbes elliptiques :

• $x_P \not = x_Q$ :
  alors , on a : $\begin{cases} s = \dfrac{y_p-y_q}{x_p-x_q} \newline x_{P+Q} = s^2 - (x_P+x_Q) \newline y_{P+Q} = s*(-s^2+x_P+x_Q)-t \end{cases}$

• $x_P = x_Q$ et $y_P \not = y_Q$ :
  alors, on a $P+P=2P=O$ , un point à l’infini

• $P = Q$ et $y_P = y_Q \not = 0$ :
  alors, on a : $\begin{cases} s = \dfrac{3x_{P}^2+a}{2y_P} \newline x_{P+Q} = s^2 - (2x_P) \newline y_{P+Q} = s(x_P-x_{2P}) -y_P \end{cases}$

• $P = Q$ et $y_P = y_Q = 0$ :
  Alors, on a $P+P=2P=O$ , un point à l’infini

La multiplication dans ce groupe est elle aussi changé:

Ainsi, si on pose:

$\begin{cases} P \in E \newline k \in Z \newline Q = k*P \newline \end{cases}$

alors, $Q =P+P+.k fois..+P$

Problème du logarithme discret.

Forme générale :

On choisit un groupe $G$ (cyclique) d’ordre $n$ engendré par un entier $g$.

Alors on a :
$\forall x \in G~,~ \exists ~ \alpha \in [0,n[ ~et ~~ x=g^{\alpha}$
Alors $\alpha$ est noté $log_g(x)$ , c’est le logarithme discret de $x$ en base $g$

La difficulté de ce problème réside dans le fait de retrouver ce $\alpha$ connaissant x et g Celle ci dépend du groupe $G$ dans lequel on travail.

Exemple: Avec G=$Z/nZ$ engendré par $g$
Alors trouver $\alpha$ revient à résoudre: $\alpha*g=x \pmod n$
ce qui est ici facilement faisable avec l’algorithme d’euclide étendu.
Source ici

Appliqué aux courbes elliptiques (ECDLP)

On cherche ici à trouver $\alpha$ tel que $\alpha*g=b$ avec les propriétés évoqués précédemment .
De nombreux algorithme existe pour tenter de résoudre cette équation :

• Baby-Step / Giant-Step
• Pohlig Hellman
• Rho Pollard
• Kangaroo Pollard
• …

Application à la cryptographie.

On se place dans une situation ou 2 individus :

• Alice
• Bob
  Souhaitent s’échanger une clé secrète afin de pouvoir chiffrer leurs futures communications.
  Afin d’empêcher un leak de leur clé secrète, ils décident d’utiliser l’échange de clé inventé par Diffie-Helhman.

Paramétrage :

Alice et Bob se sont mis d’accord au préalable sur deux choses :

• Un nombre premier $p$
• Un point $G \in E(Z/pZ)$

Ainsi, chacun choisi un entier dans $[0,p[$ et le multiplie par G , le point générateur.

Pour Bob:
$\begin{cases} a \in [0,p[ \newline A = a*G \newline \end{cases}$

Pour Alice:
$\begin{cases} b \in [0,p[ \newline B = b*G \newline \end{cases}$

A et B sont les clés publiques de Alice et Bob.

Echange des clés :

• Alice envoie B à Bob.
• Bob envoie A à Alice.

Calcul de la clé privée :

• Alice calcul $A*b$
• Bob calcul $B*a$

On a ainsi :
$K = A*b = B*a = G*(b*a)$

Voici un schéma qui représente l’échange de clés:

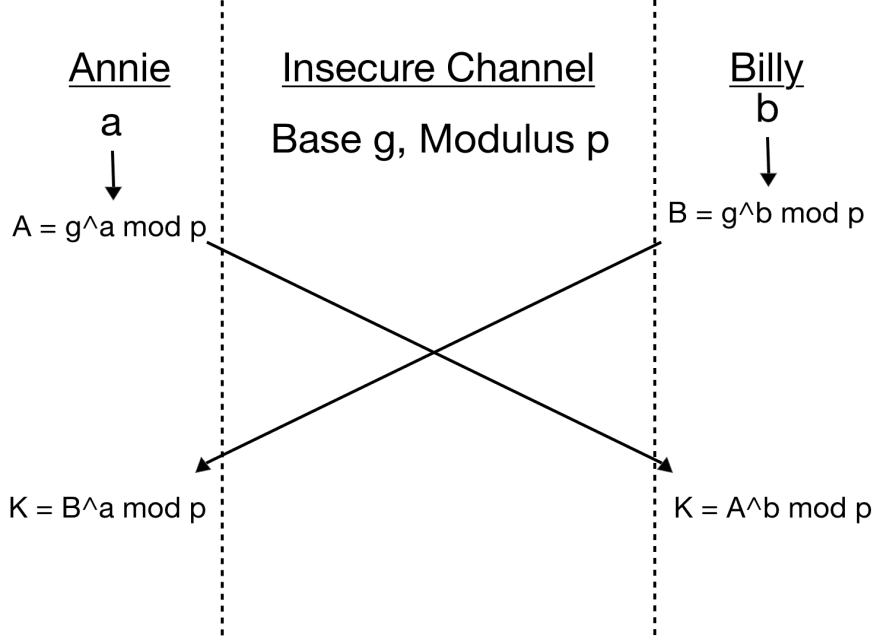
Sécurité

Toute la sécurité de cet échange de clé réside dans la difficulté à retrouver $a$ ou $b$ à partir de A, B et p. C’est à dire, résoudre le problème du logarithme discret.

Implémentation en python (SageMath)

from random import randint

## SETUP
Curve_A = -35
Curve_B = 98

# Prime Number
P = 434252269029337012720086440207

# Define a curve
E = EllipticCurve(Zmod(P),[Curve_A,Curve_B])

# Generator G
G = E([
	16378704336066569231287640165,
	377857010369614774097663166640
])

# Alice
a = randint(0,P-1)
A = a*G

# Bob
b = randint(0,P-1)
B = b*G

# Alice sent A to Bob & Bob sent B to Alice

# Alice
k1 = a*B

# Bob
k2 = b*A

# Check if keys are equals
assert k1 == k2

Attaque en utilisant la methode discrete_log de SageMath :

On peut imaginer qu’une troisième personne intercepte l’échange de clé publique, celle-ci peut tenter de retrouver une dés clé privée :

def steal_DLP_A(A,B):
	a = G.discrete_log(A)
	return B*a

ou

def steal_DLP_B(A,B):
	b = G.discrete_log(B)
	return A*b

...

k3 = steal_DLP_A(A,B)
k3 = steal_DLP_B(A,B)

assert k1 == k2 == k3 == k4