Introduction

Nous avons vu précédemment (ici) que le chiffrement RSA reposé sur 2 nombres premiers , notés $p$ et $q$. Grâce à ces deux nombres cryptographiquement grands, il était ainsi possible de générer une paires de clé $(publique/privée)$ et chiffré des messages grâce à celle-ci.

Nous allons voir ici quelques premières vulnérabilités sur le chiffrement RSA.

1) $P$ et $Q$ trop petit.

On rappèle que la clé privée est :
$d = e^{-1} \pmod {\Phi(n)}$
Avec $\Phi(n) = (p-1)(q-1)$

Un utilisateur lambda à souvent accès à sa clé publique : $n = p*q$ lui permettant de chiffrer des messages.

Ainsi, si on suppose que $p$ et $q$ sont petits , il est alors possible de les retrouver à partir de $n$ : on factorise la clé n

Si on suppose la clé publique :

n = 546480898644192854289613211318283372083827462595494488488703390642299583863737949445782560754114114083715341900177523352513320308835896569559795948842696151215075935167387324762001504175864881745474931498272994380590436716963454423950174614869590249698373859676626313904736490404029457882552069971909822348178035620519

Grâce à des outils comme factordb de retrouver les facteurs premiers .

Ici :

p = 145321011760000531877435723975947637897203583948906575807198035294184789506898084396795093090540801037567805321617481052647707027564293450643293853645681384319755797399524426379496640305781690028758116557134771373287250667442637194127844508799858005612032497781860829178150761527965250346924976527571899145109
q = 3760508491

J’ai personnellement écris un outils qui permet cette factorisation : Factor4Ctf qui utilise plusieurs technique de factorisation que nous verrons dans de prochains articles .

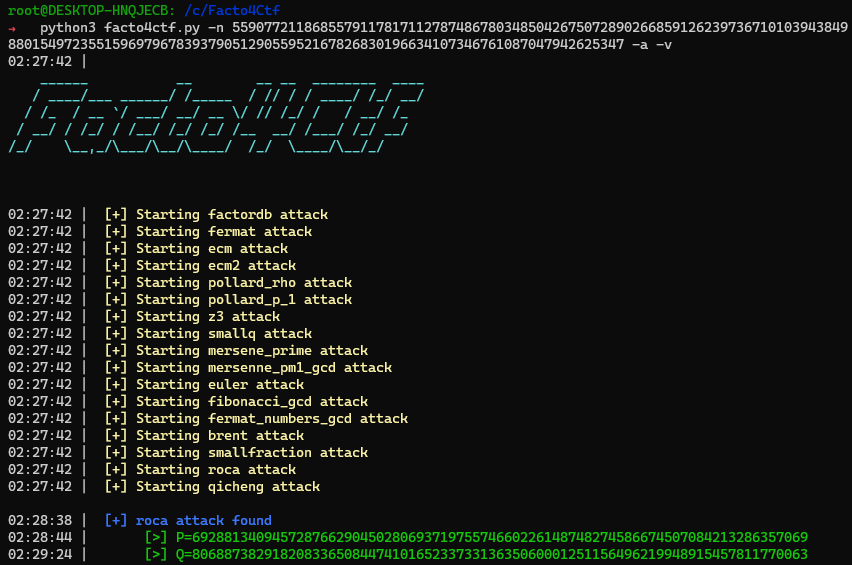
D’autre outils comme SageMath, PariGp ou encore CadoNFS permettent la factorisation de $n$ avec des facteurs allant jusque 512bits.

Avec les facteurs retrouvés, on peut recalculer la clé D et ainsi déchiffrer le message chiffré.

2) Message trop petit.

On rappelle que le message chiffré est :
$c = m^e\pmod n$.

Si on suppose que :

• $e =3$
• $m^e$ < $n$ , alors lors du chiffrement , le modulo ne s’applique pas.

On a donc : $c = m^e$ et il suffit de déchiffrer le message grâce à une racine $3^{ième}$ :
$m = c^{1/3}$

from Crypto.Util.number import long_to_bytes
import gmpy2

gmpy2.get_context().precision=99999

e = 3
m = int(gmpy2.root(c,e))
m_text = long_to_bytes(m).strip(b'\x00').decode()

3) Leak Supplémentaires.

Dans certains cas (souvent en ctf) , il est possible de retrouver les facteurs $p$ et $q$ grâce à des indices données en plus des classiques $n$ et $e$ .
Par exemple , si $\Phi(n)$ est donné ; on peut retrouver les facteurs de la manière suivante :

On a :

• $n=p*q$
• $\phi(n) = (p-1)*(q-1) = p*q - (p+q) + 1$

De plus $p$ et $q$ sont racines du polynomes suivant:

$f(x) = (x-p)*(x-q)$
$\qquad= x^2 - (p+q)*x + p*q$
$\qquad= x^2 - (n+1-phi(n))*x + n$

from math import isqrt

def attack(n,phi):
  s = - (n + 1 - phi)
  delta = s ** 2 - 4 * n  
  p = int(s - isqrt(delta)) // 2
  q = int(s + isqrt(delta)) // 2
  return (p,q)